[2025 1학기 알고리즘 스터디] 이서영 #4주차
* 파이썬으로 풀었습니다.
- 1260: DFS와 BFS
- 11724: 연결 요소의 개수
- 2178: 미로 탐색
1260. DFS와 BFS
문제
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.
제가 아는 그래프는 막대그래프밖에 없습니다. + 꼭짓점 그래프
알고리즘의 그래프 개념에 대해 공부해주겠습니다.
Graph : 정점(Vertex or Node)과 정점을 연결하는 간선(Edge)으로 구성된 자료구조
방향성 O 방향 그래프(Directed Graph)
방향성 X 무방향 그래프(Undirected Graph)
그래프 탐색 문제
: 한 그래프와 해당 그래프의 시작 정점이 주어졌을 때, 시작점에서 간선을 타고 이동할 수 있는 정점을 모두 찾아야 하는 문제
1. 깊이 우선 탐색(Depth-First Search, DFS)
: 그래프의 시작점에서 다음 브랜치로 넘어가기 전에, 해당 브랜치를 모두 탐색, Stack 이용

2. 너비 우선 탐색(Breadth-First Search, BFS)
: 그래프의 시작점에서 가까운 점들부터 우적으로 탐색, Queue 이용
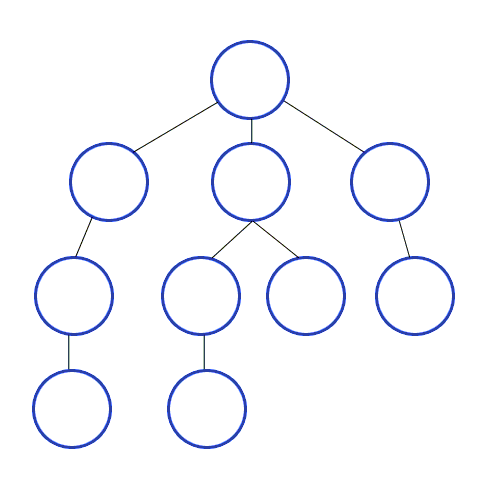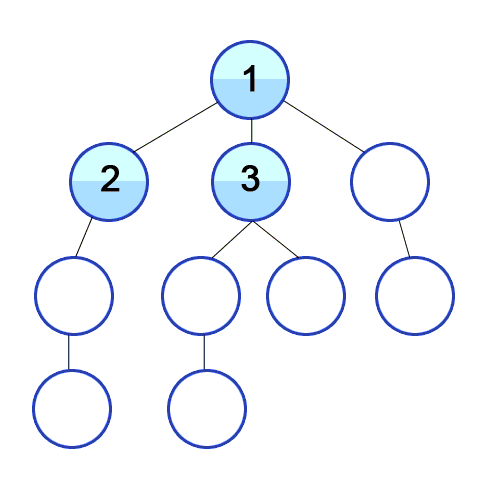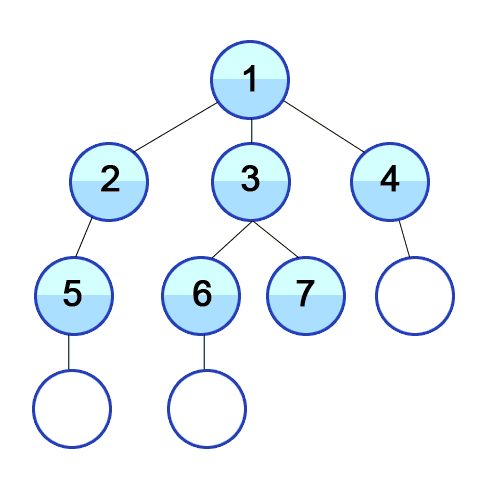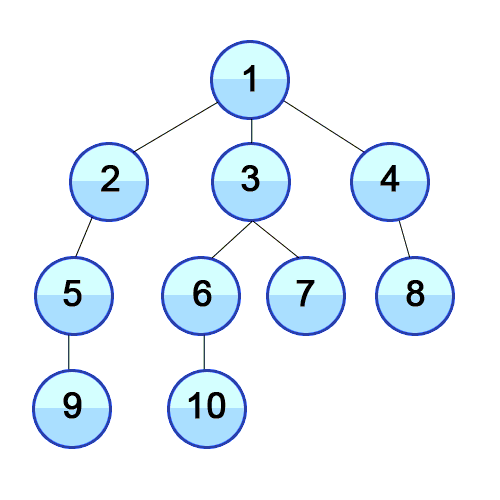
사실 이해가 안됩니다.
이럴 때 팁, 그림판 그리기
예제 입력 1
4 5 1
1 2
1 3
1 4
2 4
3 4예제 출력 1
1 2 4 3
1 2 3 4
둘째 줄부터는 간선이 연결하는 두 정점의 번호입니다. 예제 1을 바탕으로 생각해보면

이런 식으로 연결 되어있다 생각할 수 있습니다. 여기서 깊이 우선 탐색인 DFS로 수행한다면 시작 정점 번호인 1부터 연결이 끝날 때까지 계속 가는 것이라 생각했습니다.

그러면 예상 출력은 1243으로 예제 출력1의 DFS 부분과 맞습니다. 이해 완료!
BFS로도 해보겠습니다.

예상 출력 1234, 예제 출력1 BFS 부분과 일치합니다.
코드를 구현하겠습니다.
import sys
input = sys.stdin.readline
N, M, V = map(int, input().split()) # N = 정점 개수, M = 간선개수, V = 시작 정점 번호
node = [[] for _ in range(N + 1)] #인접 리스트 생성
for _ in range(M):
A, B = map(int, input().split())
node[A].append(B)
node[B].append(A)
for i in range(1, N + 1):
node[i].sort() #정렬
def DFS(start):
stack = [start]
visited = [0] * (N + 1) #정점 번호가 1번부터 N번까지여서
while stack:
v = stack.pop()
if not visited[v]:
visited[v] = True
print(v, end=' ')
for i in reversed(node[v]): #stack에서 작은 번호 먼저 pop하려면 큰 거 먼저 넣어야됨
if not visited[i]:
stack.append(i)
def BFS(start):
queue = [start]
visited = [0] * (N + 1)
visited[start] = True
front = 0
while front < len(queue):
v = queue[front]
front += 1
print(v, end=' ')
for i in node[v]:
if not visited[i]:
visited[i] = True
queue.append(i)
DFS(V)
print()
BFS(V)
11724. 연결 요소의 개수
문제
방향 없는 그래프가 주어졌을 때, 연결 요소 (Connected Component)의 개수를 구하는 프로그램을 작성하시오.
이게 머죠?
연결 요소의 규칙
- 연결 요소에 속한 모든 정점을 연결하는 경로 존재
- 또 다른 연결 요소에 속한 정점과 연결하는 경로 금지
DFS를 활용하여 코드를 구현했습니다.
import sys
input = sys.stdin.readline
N, M = map(int,input().split())
node = [[] for _ in range(N + 1)] #인접 리스트
visited = [0] * (N + 1) #정점 i를 방문했는지 여부, 0이면 방문 X
#N + 1인 이유는 정점이 1번부터 시작해서 0번 인덱스는 사용 X
for _ in range(M):
u, v = map(int,input().split())
node[u].append(v)
node[v].append(u)
def DFS(v):
visited[v] = True #정점 v를 방문 표시
for u in node[v]:
if not visited[u]: #v와 연결된 정점 u 중에서 방문하지 않은 정점을 재귀적 탐색
DFS(u)
count = 0
for i in range(1, N + 1):
if not visited[i]:
DFS(i)
count += 1
print(count)
2178. 미로 탐색
문제
N×M크기의 배열로 표현되는 미로가 있다.
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 |
미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1, 1)에서 출발하여 (N, M)의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 프로그램을 작성하시오. 한 칸에서 다른 칸으로 이동할 때, 서로 인접한 칸으로만 이동할 수 있다.
위의 예에서는 15칸을 지나야 (N, M)의 위치로 이동할 수 있다. 칸을 셀 때에는 시작 위치와 도착 위치도 포함한다.
최소 이동 칸을 구해야하니 DFS보다는 BFS로 푸는 게 더 좋다고 생각했습니다.
import sys
from collections import deque
input = sys.stdin.readline
N, M = map(int, input().split())
maze = [list(map(int, input().strip())) for _ in range(N)]
dx = [-1, 1, 0, 0] #방향벡터 위 아래
dy = [0, 0, -1, 1] #왼 오
def BFS(x, y):
queue = deque()
queue.append((x, y))
while queue: #큐가 채워져 있는 동안 계속 탐색
x, y = queue.popleft() #현재 위치 (x,y) 꺼내기
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if nx < 0 or nx >= N or ny < 0 or ny >= M: #미로 바깥은 무시
continue
if maze[nx][ny] == 0: #벽
continue
if maze[nx][ny] == 1:
maze[nx][ny] = maze[x][y] + 1
queue.append((nx, ny))
return maze[N - 1][M - 1]
print(BFS(0, 0))

후기
자료구조 열심히 들을걸...
자료구조 때 스택과 큐를 배우며 간단히 배웠던 DFS, BFS 개념을 좀 더 자세히 공부하는 느낌이었습니다. 근데 어려워요. 엄청 어려워요. 생각은 쉬운데 구현이 익숙지가 않으면서 많이 어려운 것 같습니다. 더 공부해야 할 필요성을 느꼈습니다.