1. 1로 만들기
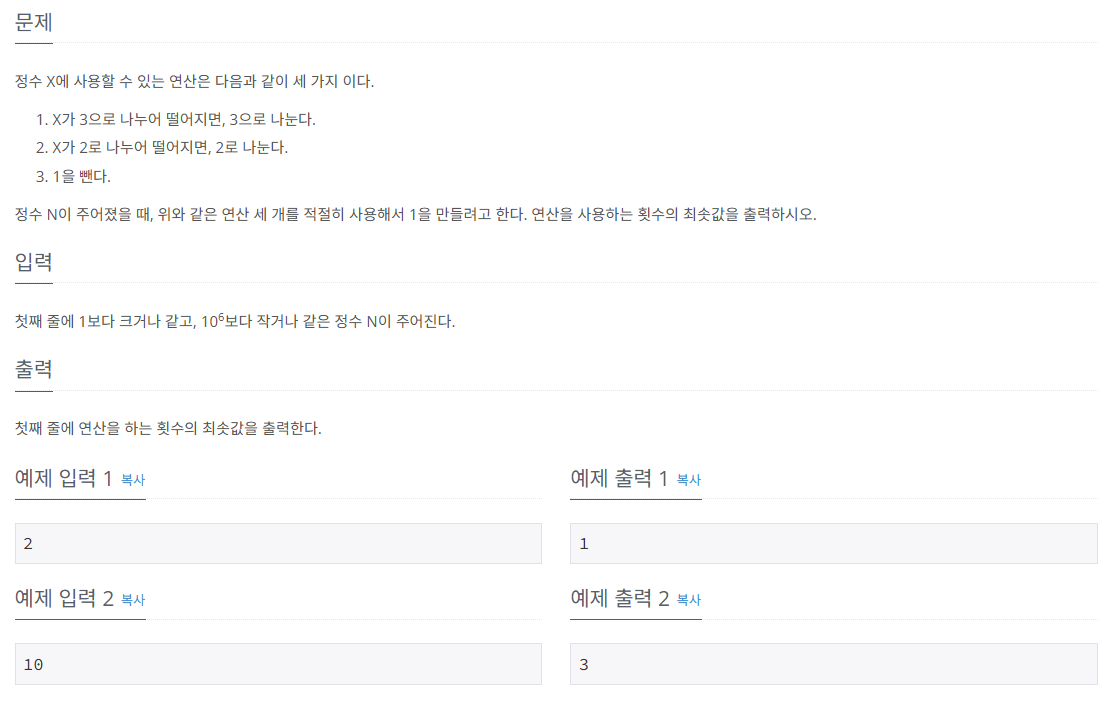
연산을 최소한으로 사용하여 정수 x를 1로 만드는 문제이다.
3의 배수인 경우 3으로 나누기, 2의 배수이면 2로 나누기, 1을 빼주는 연산중에 선택할 수 있다.
입력된 정수를 위의 과정중 하나를 선택하여 연산하여야하는데 2의 배수나 3의 배수 둘다 아닌 경우는 1을 빼주는 것이 자명해 보인다.
3의 배수이면 3으로 나누어주는 것이 가장 좋아보인다. 1로 만드는 과정에서 수를 최대한 줄여야하는데 3가지 과정중에 3으로 나누어 주는 것이 가장 수를 작게 만드는 방법이기 때문이다.
문제는 2의 배수인 경우이다. x가 10인 경우 2로 나누어 (10 -> 5 -> 4 -> 2 -> 1) 계산하는 방법보다 (10 -> 9 -> 3 -> 1)이 최소한으로 계산하는 경우이이 때문이다. 따라서 -1을 해주어 3의 배수이면 2로 나누어 주는 것이 아니라 -1 연산을 해주고 아닌 경우 2로 나누어 주었다.
import sys
input = sys.stdin.readline
num = int(input())
count = 0
while True:
if num == 1:
break
else:
if num % 3 == 0:
num /= 3
count += 1
elif num % 2 == 0:
if (num - 1) % 3 == 0:
num -= 1
count += 1
else:
num /= 2
count += 1
else:
num -= 1
count +=1
print(count)
정답을 입력후 제출했더니 실패가 나왔다.
왜 틀렸는지 살펴보면서 최소계산으로 1을 만들어야한다는 점에 주목했다.
(2의 배수일때만 주목)
만약 두번 계산을 진행한다고 가정하면 2로 두번 나누어 주거나(4의 배수인 경우) 1을 한번 빼주고 3을 나누는 경우 사이에 전자가 가장 작은 수로 만들어주므로 2로 두번 나누어주는 경우로 생각한다.
♣ 최대한 작은 수로 만들려함 (문제가 되는 2의 배수인 경우를 생각, 3의 배수라면 무조건 3으로 나누어줌)
2로 나누기 -> 1을 빼주기(2, 3의 배수도 아님) vs 1빼주기 -> 3로 나누기
-------->> 1빼고 3나누기 (전자의 경우보다 작게 만들어주기 때문)
2로 나누기 -> 2로 나누기 vs 1 빼주기 -> 3로 나누가
--------->> 2로 나누기 -> 2로 나누기 (이하동문)
2로 나누기 -> 2로 나누기 -> 2로 나누기 vs 1 빼주기 -> 3로 나누기 -> 3로 나누기
--------->> 후자 (이하동문)
이런 논리로 코드를 작성하니
import sys
input = sys.stdin.readline
num = int(input())
count = 0
while True:
if num == 1:
break
else:
if num % 3 == 0:
num /= 3
count += 1
elif num % 2 == 0:
n_2 = num
c2 = 0 #c2는 2가 총 몇번 곱해져 있는지 확인하기 위함
n_3 = num - 1
c3 = 0 #c3은 num 에다가 1을 빼준후 3이 몇번 곱해져 있는지 확인하기 위함
while n_2 % 2 == 0:
n_2 /= 2
c2 += 1
while n_3 % 3 == 0:
n_3 /= 3
c3 += 1
if c3 == 0 or (c2 >= 2 and c3 == 1):#num -1 을 한 값이 3으로 떨어지지 않거나 2로 계속나누어주는것이 최선일 때
num /= 2
count += 1
else:
num -= 1
count += 1
else:
num -= 1
count +=1
print(count)
예....... 오답!!
흠....... 아 어디가 틀렸을까...... 3의 배수일때 3의 배수로 나누어주지 않을 때도 존재하는가......
DP를 사용하지 않고 풀기가 불가능한 것 같았다.
DP(다이나믹 프로그래밍)
앞에서 계산한 식을 배열에 미리 저장하여 연산속도를 증가시키는 프로그래밍이다.
중복해서 계산하거나 값이 존재하는 문제들을 존재할 때 중복 호출이 발생하지 않게 함으로써 최적화를 도와준다.
DP에는 크게 바텀업방식과 탑다운 방식이 있다.
바텀업 방식은 주로 DP에서 사용하는 방식으로 하위 문제부터 차례대로 계산하여 큰 문제를 푸는 방식이다.
테이블 크기가 문제 크기이므로 메모리사용 예축이 쉽고 중복호출이 없으므로 오버플로우도 없고 빠르다.
또한 계산이 순차적이라는 점 때문에 이해하기 쉽다.
탑다운 방식은 큰 문제부터 시작해서 하위문제를 재귀적으로 해결하는데 계산한 결과는 저장하는 방식이다. 재귀함수와 메모이제이션을 사용한다. 간결하고 재귀적 사고에 적합하나 스택 초과 위험이 있다.
예를 들어 피보나치 수열을 다이나믹 프로그래밍으로 표현할 수 있다.
#dp사용하지 않고 재귀만 사용
def fibo(x):
if x == 1 or x == 2:
return 1
return fibo(x-1) + fibo(x-2)
print(fibo(4)) #3
위의 코드는 재귀함수로 작성된 피보나치 수열이다. 얼핏보면 간단하고 최적화된 코드로 보인다.
하지만 fibo(10)값을 찾는다고 가정해보자. fibo(9)과 fibo(8)을 호출하여야하고 다시 fibo(9)과 fibo(8)값에 대해서도 하위 fibo를 다시한번 호출해야한다. 이 과저에서 하위fibo가 중복호출되는 일이 발생하고 지수시간복잡도를 가지게 된다.
#dp 다운업방식
fibo = [0] * 100
fibo[1] = 1
fibo[2] = 1
for i in range(3, 100):
fibo[i] = fibo[i-1] + fibo[i-2]
print(fibo[99])
0으로 초기화된 배열을 만든후 차례대로 그 배열을 다운업 방식으로 채워나간 코드이다.
재귀함수로 작성된 코드와 달리 fibo[99]를 구할때 fibo[98] + fibo[97]을 해주는데 fibo[98], fibo[97]값이 숫자로 존재하기 때문에 다시 구하는 과정이 필요없다.
#dp 탑다운방식
d = [0] * 100
def fibo(x):
if x == 1 or x == 2:
return 1
if d[x] != 0:
return d[x]
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
print(fibo(99))
재귀함수를 사용하긴하나 메모이제이션을 사용하여 연산결과를 기억하기 때문에 재귀함수로만 작성한 코드보다 빠르다. 하지만 파이썬 재귀 깊이 제한 때문에 너무큰수는 오류가 발생할 수 있다는 점이 있다.
import sys
input = sys.stdin.readline
x = int(input())
way_1 = [0] * (x+1)
for i in range(2, x+1):
way_1[i] = way_1[i-1] + 1
if i % 2 == 0:
way_1[i] = min(way_1[int(i/2)] + 1, way_1[i])
if i % 3 == 0:
way_1[i] = min(way_1[int(i/3)] + 1, way_1[i])
print(way_1[x])
위와 같이 깔끔하게 1로 만들기 문제를 풀었다.
2. 계단 오르기

계단을 오르는데 최대 점수를 구하는 문제이다.
DP를 사용하기 위하기 위해 각 계단층이 가질 수 있는 최대값에 해당하는 배열을 만들면서 시작했다.
import sys
input = sys.stdin.readline
time = int(input())
stairs = [0] #각 계단이 가지는 값 0을 먼저 너준 이유는 i층에 해당하는 값을 stairs[i]로 호출하기 위함
s_stair = [0] * (time + 2) #계단이 가지는 누적 최대 값
for _ in range(time):
num = int(input())
stairs.append(num)
# 계단 값을 넣어줌
s_stair[1] = stairs[1]
if time == 1:
print(s_stair[1]) # 1층만 존재하는 경우 아래 경우가 범위오류가 나기 때문에 조건문 사용
else:
s_stair[2] = stairs[2] + stairs[1]
for i in range(3, time + 1):
s_stair[i] = max(s_stair[i-3]+stairs[i-1]+stairs[i], s_stair[i-2]+stairs[i])
print(s_stair[time])

i 번째 계단에서 가질 수 있는 경우의 수는 위의 경우와 같이 빨간색과 파란색 방법이 있다.
빨간색 방법의 경우 i - 2 층에서의 누적값( ?최대값)에대가 i번째 계단 값을 더한 것이고
파란색 방법의 경우 i - 3층에서의 누적 최대값에대가 i번째와 i - 1번째 계단 값을 더한값이다.
즉 빨간색 방법과 파란색 방법중에서 더 큰 값을 선택하여 s_stair[ ]에다가 저장하여 dp로 풀었다.
짜잔~~~
3. 가장 긴 증가하는 부분 수열

가장 긴 증가하는 부분 수열을 구하는 문제인다.
위의 예제인 경우 (10-> 20 -> 30 -> 50) ----> 4
import sys
input = sys.stdin.readlines
n = int(input())
n_list = list(map(int, input().split()))
dp = [1] * n
for i in range(1, n):
for j in range(i):
if a[j] < a[i]:
dp[i] = max(dp[i], dp[j] + 1)
print(max(dp))
각 수열안의 인덱스에 해당하는 배열을 만든후 점차 계산해가는 방법으로 풀이를 진행했다.
마치며..
dp를 배우면서 중복계산이 필요한 문제들을 효율적으로 처리하기에 dp가 적합하다는 것을 느꼈고 실전에서도 많은 사용을 할것 같았다.
'WINK-(Web & App) > 알고리즘 스터디' 카테고리의 다른 글
| [2025 1학기 알고리즘 스터디] 박현빈 #2주차 (0) | 2025.04.09 |
|---|---|
| [2025 1학기 알고리즘 스터디] 김민재 #2주차 (0) | 2025.04.09 |
| [2025 1학기 알고리즘 스터디] 김민주 #2주차 (0) | 2025.04.08 |
| [2025 1학기 알고리즘 스터디] 이서영 #2주차 (0) | 2025.04.08 |
| [2025 1학기 알고리즘 스터디] 남윤찬 #2주차 (0) | 2025.04.06 |


