3주차 알고리즘 스터디 시작합니다.
이번주에 공부할 알고리즘 개념은 Greedy입니다!
Greedy란?
현재 상황에서 가장 좋아 보이는 선택을 하는 방식입니다.
Greedy 뜻 자체가 욕심이라 탐욕 알고리즘이라고 부르기도 하는데
매 순간마다 하는 선택은 최선이지만 전체적으로 그 선택이 최적의 선택은 아닐 수도 있습니다.
아무튼 이 알고리즘 개념으로 문제들을 풀어봅시다.
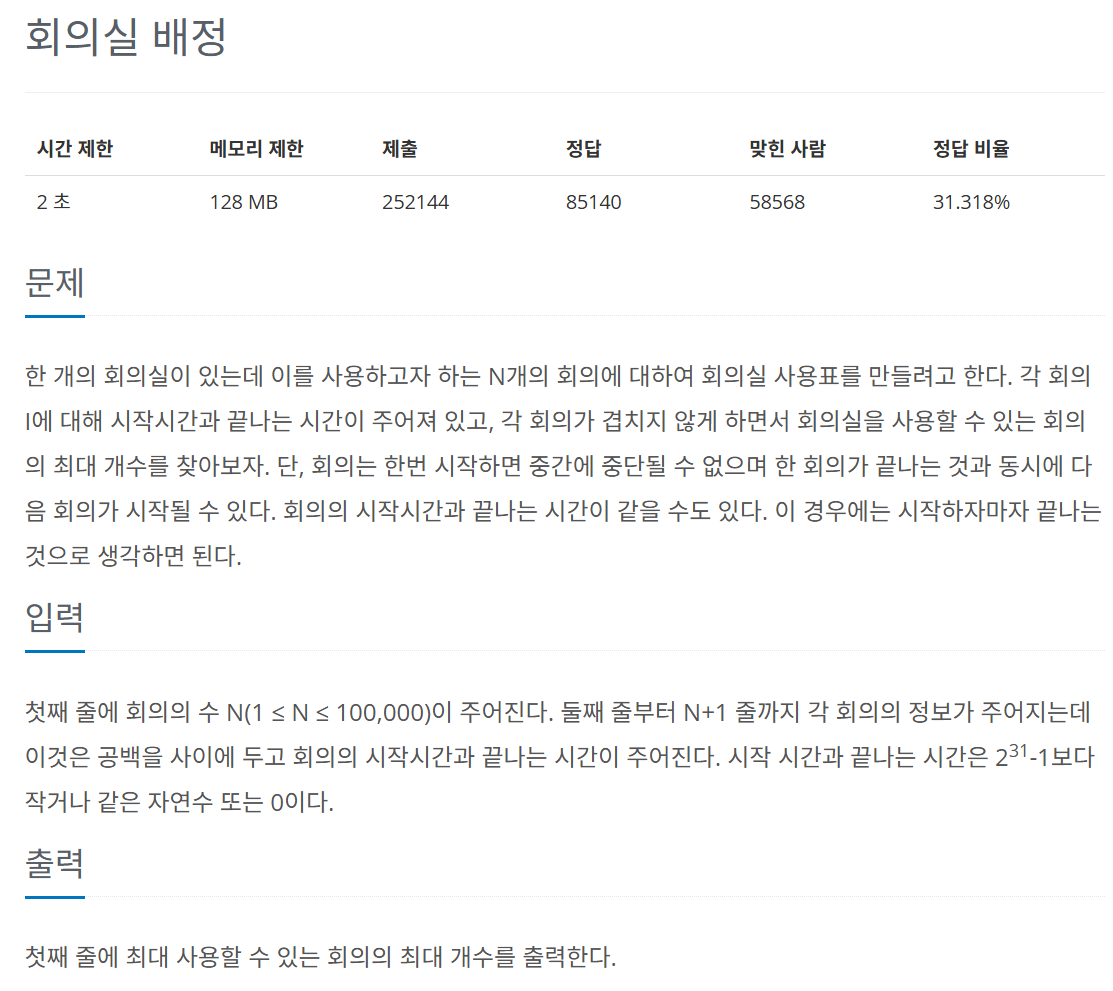
1. 회의실 배정
https://www.acmicpc.net/problem/1931
#include <iostream>
using namespace std;
int main() {
int meet;
cin >> meet;
int meetings[100000][2];
for (int i = 0; i < meet; ++i) {
cin >> meetings[i][0] >> meetings[i][1];
}
for (int i = 0; i < meet - 1; ++i) {
int minNum = i;
for (int j = i + 1; j < meet; ++j) {
if (meetings[j][1] < meetings[minNum][1]) {
minNum = j;
}
else if (meetings[j][1] == meetings[minNum][1]) {
if (meetings[j][0] < meetings[minNum][0]) {
minNum = j;
}
}
}
int tmp0 = meetings[i][0];
int tmp1 = meetings[i][1];
meetings[i][0] = meetings[minNum][0];
meetings[i][1] = meetings[minNum][1];
meetings[minNum][0] = tmp0;
meetings[minNum][1] = tmp1;
}
int currentEnd = 0;
int count = 0;
for (int i = 0; i < meet; ++i) {
if (meetings[i][0] >= currentEnd) {
currentEnd = meetings[i][1];
count++;
}
}
cout << count << '\n';
return 0;
}코드를 제출하고 시간 초과가 나왔습니다. 연산의 횟수가 너무 많아서 그런 것 같습니다.
시간 초과를 해결하려면 정렬을 위해 qsort()를 사용하는게 좋다고 하네요.
#include <iostream>
#include <cstdlib> //qsort 함수 사용을 위해 필요
using namespace std;
int meetings[100000][2];
//qsort의 비교 함수
int compare(const void* a, const void* b) {
int* meetingA = (int*)a;
int* meetingB = (int*)b;
if (meetingA[1] == meetingB[1]) {
return meetingA[0] - meetingB[0]; //시작 시간이 빠른 순으로
}
return meetingA[1] - meetingB[1]; //끝나는 시간이 빠른 순으로
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; ++i) {
cin >> meetings[i][0] >> meetings[i][1];
}
qsort(meetings, n, sizeof(meetings[0]), compare);
int count = 0;
int currentEnd = 0;
for (int i = 0; i < n; ++i) {
if (meetings[i][0] >= currentEnd) {
currentEnd = meetings[i][1];
count++;
}
}
cout << count << '\n';
return 0;
}
회의실 배정이 Greedy 알고리즘을 사용해야 하는 이유:
한 회의가 끝나자마자 다음 회의를 바로 시작할 수 있기 때문에 겹치지 않게 최대한 많은 회의를 배정해야 합니다.
이때 어떻게 회의를 고를지 생각해 보면 가능한 한 더 많은 회의를 할 수 있도록 껴(?) 넣는다..?
그렇다고 짧은 회의를 우선으로 선택하는게 아니라 가장 빨리 끝나는 회의를 먼저 선택하는 방법을 선택해야 합니다.
Greedy 알고리즘을 사용하면 전체를 다 살펴보지 않고 끝나는 시간을 보고 가장 빠른 회의를 알아낼 수 있습니다.
2. 잃어버린 괄호
https://www.acmicpc.net/problem/1541

#include <iostream>
#include <string>
using namespace std;
int main() {
string expr;
cin >> expr;
int result = 0;
int temp = 0; //덧셈 결과 저장
string num = ""; //현재 숫자 문자열
bool subtract = false; //현재 상태: 뺄셈 구간 여부
for (int i = 0; i <= expr.length(); ++i) {
if (i == expr.length() || expr[i] == '+' || expr[i] == '-') {
temp += stoi(num);
num = "";
if (expr[i] == '-' || i == expr.length()) {
if (subtract) result -= temp;
else result += temp;
temp = 0;
if (i < expr.length() && expr[i] == '-') {
subtract = true;
}
}
} else {
num += expr[i];
}
}
cout << result << '\n';
return 0;
}잃어버린 괄호에 Greedy 알고리즘을 사용해야 하는 이유:
수식에 괄호를 쳐서 결과값을 최소로 만들어야 하는데 괄호를 적절하게 치고 가장 큰 값을 빼야 결과가 최소가 됩니다.
그리고 앞으로 오는 값을 최대한 많이 묶어야 합니다.
- 뒤에 오는 모든 수를 묶어서 한 번에 빼면 가장 작은 값을 만들 수 있습니다.
이렇게 앞 뒤 계산을 생각하지 않고 현재 가장 최적인 선택을 하는 Greedy를 사용하는 적절합니다.
3. 동전 0
https://www.acmicpc.net/problem/11047

#include <iostream>
using namespace std;
int main() {
int numCoin, amount;
cin >> numCoin >> amount;
int coinValues[10];
for (int i = 0; i < numCoin; ++i) {
cin >> coinValues[i];
}
int coinCount = 0;
for (int i = numCoin - 1; i >= 0; --i) {
if (amount == 0) break;
coinCount += amount / coinValues[i];
amount %= coinValues[i];
}
cout << coinCount << endl;
return 0;
}동전 0에 Greedy 알고리즘을 사용하는 이유:
이 문제에서 항상 큰 가치의 동전을 먼저 많이 사용하는 방법이 전체 동전 개수를 줄이는 데 효과적입니다.
모든 동전은 앞의 동전의 배수이고 1, 5, 10, 50, 100, 500...처럼 이 구조에서 큰 동적을 먼저 쓰는 것이 작은 동전을 여러 개 쓰는 것보다 효율적입니다. 큰 동전부터 최대한 쓰는 게 항상 최적이므로 Greedy를 사용할 필요가 있습니다!
3주차 알고리즘 스터디 끝 !-!
'WINK-(Web & App) > 알고리즘 스터디' 카테고리의 다른 글
| [2025 1학기 알고리즘 스터디] 김민주 #3주차 (0) | 2025.05.07 |
|---|---|
| [2025 1학기 알고리즘 스터디] 이서영 #3주차 (0) | 2025.05.07 |
| [2025 1학기 알고리즘 스터디] 박현빈 #3주차 (0) | 2025.05.07 |
| [2025 1학기 알고리즘 스터디] 박건민 #3주차 (0) | 2025.05.07 |
| [2025 1학기 알고리즘 스터디] 김민재 #3주차 (0) | 2025.05.07 |


