1. DP 알고리즘
- 개념
DP(다이내믹 프로그래밍) 즉 동적인 프로그래밍이란 뜻이다.
DP를 사용하는 근본적인 이유는 복잡하고 어려운 큰 문제를 작은 문제로 쪼개서 효율적으로 풀기 위함이다.
- 예시
ex) 여러가지 무게의 물건들이 존재한다. 이때 5kg까지 들어갈수 있는 가방에 최대로 들어가는 무게는 몇 kg 인가?
위와 같은 문제를 경우의 수를 부분집합별로 다 따져서 구할 수 있다.
아마도 물건의 개수를 n이라고 가정하면 2^n개의 부분집합이 생길 것 같다.
적은 수의 물건에서는 별 문제가 되지 않겠지만 물건의 개수 즉 n의 값이 1000000(백만)개가 있다고 해보면 2^1000000 개의 부분 집합을 찾아야한다. 이러한 계산을 직접할 용기있는 사람은 몇 없을 것이다.
하지만 DP를 활용한다면, 이렇게 생각해볼수 있다.
5kg 가방에 들어갈수있는 최대값은 [4kg 가방에 들어갈수있는 최대값] + 어떤수
6kg 가방에 들어갈수있는 최대값은 [5kg 가방에 들어갈수있는 최대값] + 어떤수
7kg 가방에 들어갈수있는 최대값은 [6kg 가방에 들어갈수있는 최대값] + 어떤수
작은 kg가방 문제들의 결과값을 활용하여 더 큰 kg 가방의 문제를 해결 할 수 있는 것이다.
- 결론
DP는 작은 문제를 활용해서 큰 문제를 해결하는 "점화식" 을 세워 점화식들을 계산한뒤에 결과값을 도출하는 것이다.
이렇게 해야 안그래도 많은 수의 계산을하는 문제에서 "중복 계산"을 방지(제일 중요) 할 수 있다.
2. 문제 1
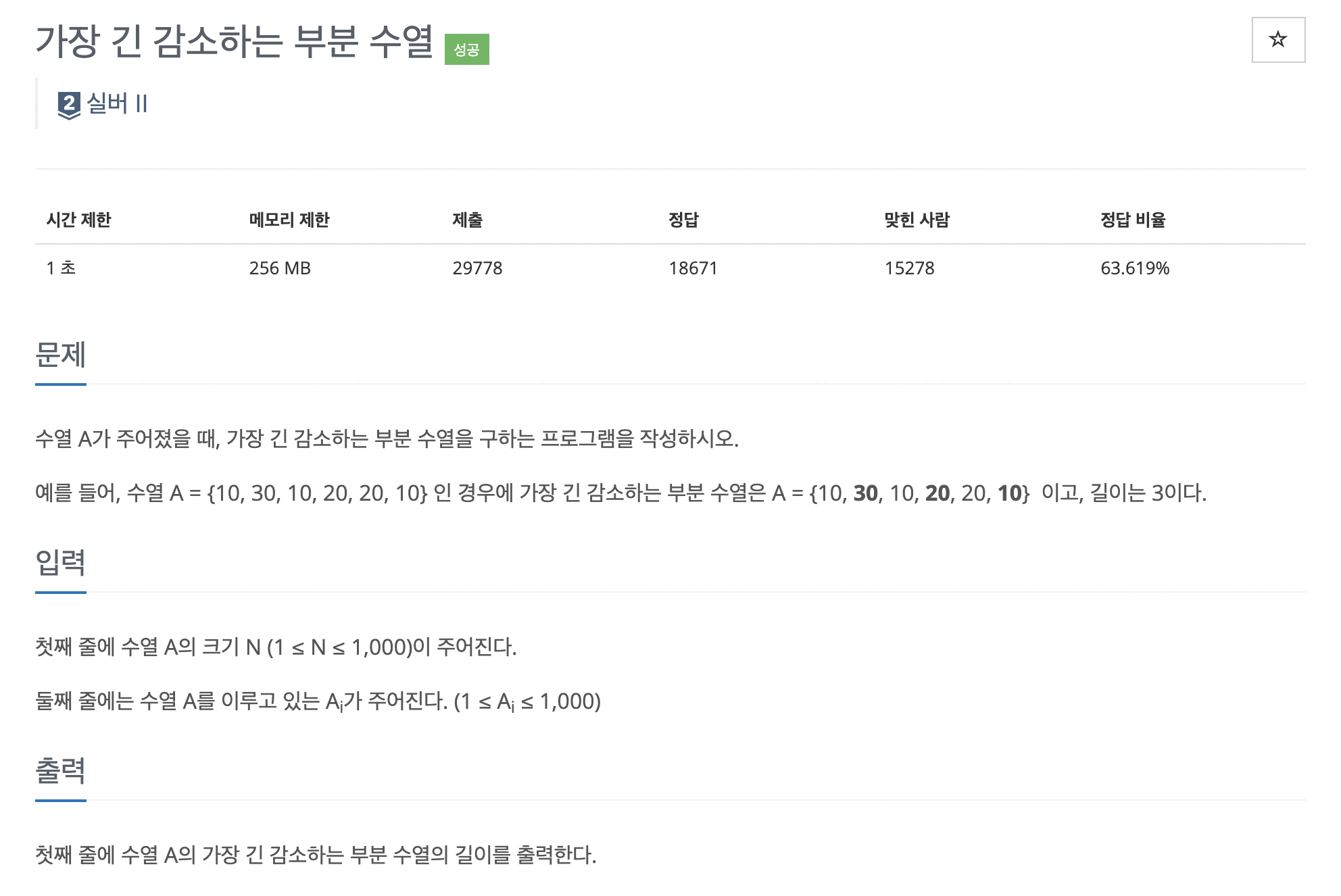
문제 설명
말그대로 가장 긴 감소하는 부분을 구해서 그 길이를 출력하면 된다.
하지만 연속으로 감소하는 부분만을 정답이라고 생각하고 푼다면 나 처럼 계속 틀릴 것이다.
예를들어 [10, 30, 5, 4, 3] 이라는 수열이 있으면 연속으로 감소하는 구간인 (5, 4, 3) 즉 3의 길이가 정답이 아니라,
(10, 30(pass), 5, 4, 3) 길이 4가 정답이다. 30은 길이 추가 x.
이를 꼭 인지하고 풀어야한다!
풀이
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int arr[1001];
int dp[1001];
int main(){
cin.sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
// 배열 입력 받기
for(int i=0; i<n; i++){
cin >> arr[i];
}
int out = 0;
// DP 사용하면서 긴 구간 탐색
for(int i=0; i<n; i++){
dp[i] = 1;
for(int j=0; j<i; j++){
if(arr[i] < arr[j]){
dp[i] = max(dp[i], dp[j] + 1);
}
}
out = max(out, dp[i]);
}
cout << out << endl;
}
dp[i]가 의미하는 것은 i번째 index까지 계산했을때 제일 길었던 감소하는 구간의 길이 이다.
dp[i]를 구하는 코드를 설명하자면,
1. i 즉 현재의 index 보다 작은 index의 값을 for문으로 돌면서 이전에 있었던 수열 값들 을 확인한다.
2. 이때 이전의 수열 값들이 더 클 경우 그 곳의 index가 j인데 이때,
dp[i]값과 더 큰 수열이 있던 j라는 index의 dp[j] + 1(현재 i번째 위치를 포함하는 것임) 을 비교해서 더 큰값으로 갱신한다.
쉽게 말해서 지나온 값들 보면서 계속해서 어떤 수열 다음으로 했을때 최대 길이가 되는지 확인하는 작업이다!
3. 문제 2
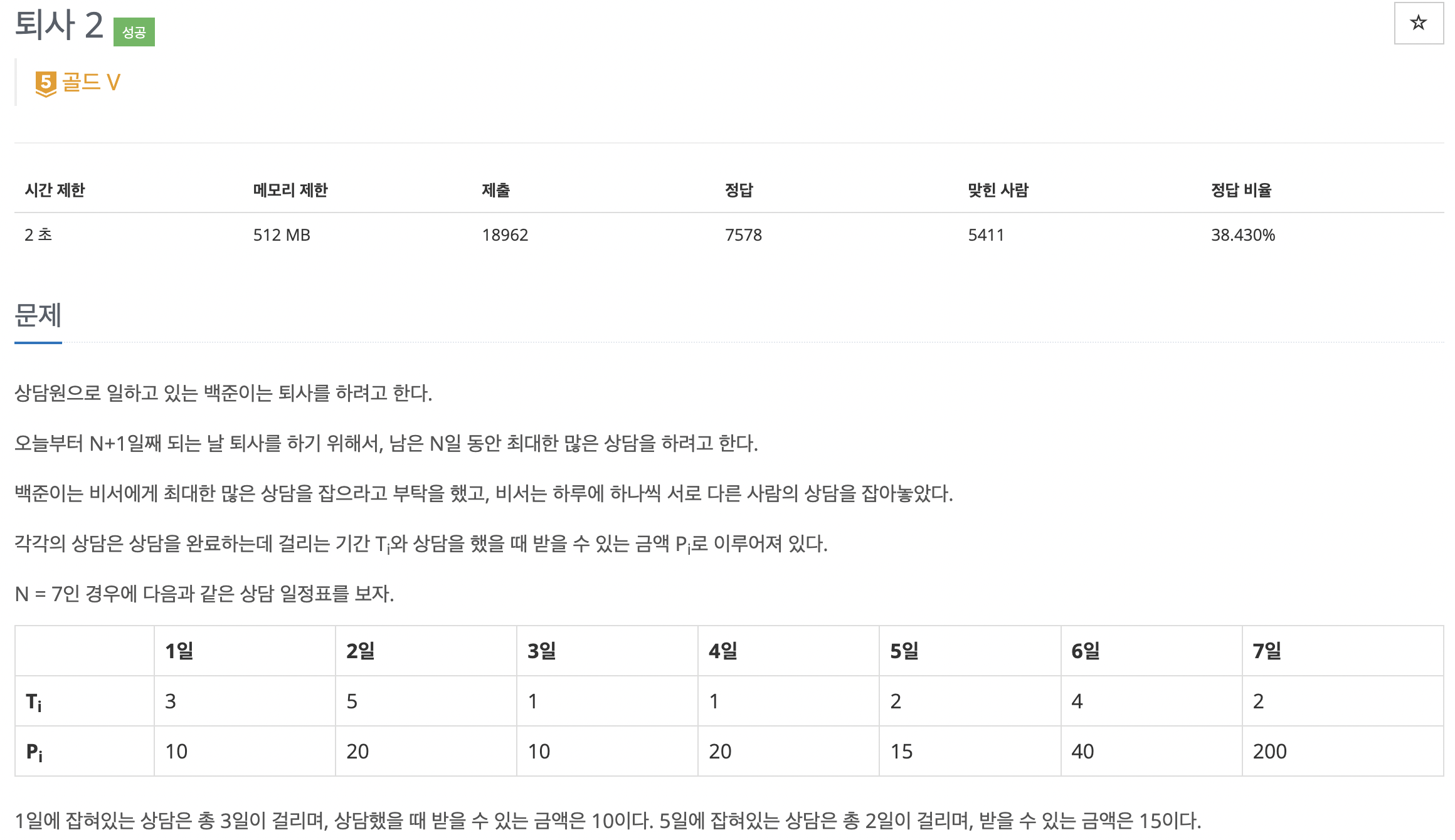

문제 설명
퇴사하기 전까지 끝낼수있는 상담들을 어떻게 해야 최대로 돈을 벌수 있는지에 관한 문제이다.
7일날 하루걸리는 상담을 한다면 7일 당일에 끝나는 걸로 생각해야한다.
이때, 7일에 끝나더라도 정산 받는 날은 그 다음날인 8일로 생각해 주어야 한다.
풀이
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int t[1500002];
int p[1500002];
int dp[1500002];
int n;
int main(){
cin >> n;
for(int i=0; i<n; i++){
cin >> t[i];
cin >> p[i];
}
// DP
int pay_day;
for(int i=0; i <= n+1; i++){
pay_day = i + t[i];
// 퇴사전에 끝낼 수 있는 상담일 경우
if(pay_day < n+1){
dp[pay_day] = max(dp[i] + p[i], dp[pay_day]);
}
// 다음날에 정산하기
dp[i+1] = max(dp[i], dp[i+1]);
}
cout << dp[n+1] << endl;
}
코드를 보면 풀이는 생각보다 간단하다.
우선 문제에서 N의 값이 최대 1,500,000 까지 주어지는데, 이 모든 부분집합을 다 계산하기 힘들어서 DP를 사용해야한다는 게 눈에 보여야 한다.
1. 모든 날을 순서대로 탐색하면서 그날에 들어오는 상담 일정이 퇴사 전에 끝낼 수 있는지 확인한다.
2. 만약 끝낼수 있는 상담이 들어왔다면 dp[pay_day](해당 상담이 끝나는날에 최대 수익금)의 값을 dp[i](현재까지 최대 수익금) + 오늘들어온 상담 수익금 으로 설정 해준다.
3. 2번의 로직을 진행할때 이전에 어떤 날에서 중복으로 pay_day날의 dp값을 설정했을 수도 있으니 max를 사용해 비교해주어야 한다.
4. 마지막으로, 다음날의 dp 값을 정산할때 미리 설정된 dp 값과 현재까지의 dp 값중 max 값을 설정해서 정산해준다.
'WINK-(Web & App) > 개인 스터디 & 프로젝트' 카테고리의 다른 글
| 알고리즘 2인 스터디 #2주차 - 박성훈 (1) | 2023.07.25 |
|---|---|
| 알고리즘 2인 스터디 #2주차 - 이총명 (0) | 2023.07.25 |
| [Node.js & React.js] 인프런 강의 듣기(2) (0) | 2023.07.21 |
| 알고리즘 2인 스터디 #1주차 - 박성훈 (0) | 2023.07.18 |
| 알고리즘 2인 스터디 #1주차 - 이총명 (0) | 2023.07.18 |



